1、解释PCA的主要思想,并说明在降维过程中,如何选择主成分数量的合适值?同时,PCA是否可以应用于非线性数据?
面试官: 你好,小壮。首先,请解释一下PCA的主要思想是什么?
小壮: PCA,即主成分分析,旨在通过线性变换将原始数据映射到一个新的坐标系,使得在新坐标系下数据的方差最大化。这个新坐标系的基底由数据的主成分构成,第一个主成分对应的方向是数据中方差最大的方向,依次类推。
面试官: 很好,那在降维过程中,如何选择主成分数量的合适值呢?
小壮: 这是一个关键问题。我们通常通过观察方差的解释程度来决定选择多少个主成分。具体而言,我们计算每个主成分的方差解释比例,即该主成分对总方差的贡献。然后,我们可以设置一个阈值,保留那些累积方差贡献达到阈值的主成分数量。
面试官: 能否用一个具体的例子来说明呢?
小壮: 当然!假设我们有一个3维数据集,我们通过PCA得到了三个主成分,对应的方差解释比例分别是0.8、0.15、0.05。如果我们设置阈值为0.95,那么我们就会保留前两个主成分,因为它们的累积方差解释比例为0.8+0.15=0.95,满足我们的设定阈值。
面试官: 那 PCA 是否可以应用于非线性数据呢?
小壮: PCA的确是基于线性变换的,但可以通过核技巧(kernel trick)将其拓展到非线性数据。这时候我们可以使用Kernel PCA。简单来说,它使用核函数将数据映射到更高维的空间,然后在该高维空间中进行PCA。最常用的核函数包括多项式核和径向基函数(RBF)核。
面试官: 能否给个例子,演示一下Kernel PCA 的计算步骤?
小壮: 好的!
首先,RBF核的公式为$K(\mathbf{x}_i, \mathbf{x}_j) = \exp\left(-\frac{|\mathbf{x}_i – \mathbf{x}_j|^2}{2\sigma^2}\right)$,其中$\sigma$是核函数的带宽参数。我们可以先计算得到核矩阵。
接下来,我们计算中心化的核矩阵$K’$,其公式为$K’ = K – \mathbf{1}\cdot K – K\cdot \mathbf{1} + \mathbf{1}\cdot K\cdot \mathbf{1}$,其中$\mathbf{1}$是全1矩阵。
然后,我们对中心化的核矩阵$K’$进行特征值分解,得到特征值$\lambda$和对应的特征向量$\mathbf{v}$。这一步可以用下面的公式表示:
$$
K’\mathbf{v} = \lambda \mathbf{v}
$$
面试官: 明白。特征值和特征向量得到了,接下来呢?
小壮: 接下来,我们选择前k个最大的特征值对应的特征向量,构成一个矩阵$V_k$。这个矩阵就是我们降维后的数据在新空间的表示。
面试官: 降维后的数据怎么计算呢?
小壮: 我们将原始数据$\mathbf{X}$投影到新的空间,得到降维后的数据$\mathbf{X}{\text{kernel_pca}}$。 投影的计算公式为:
$$
\mathbf{X}{\text{kernel_pca}} = \mathbf{K’}\cdot \mathbf{V}_k
$$
这里的$\mathbf{K’}$是原始数据的中心化核矩阵,$\mathbf{V}_k$是选取的前k个特征向量组成的矩阵。
面试官: 非常清楚。感谢你的详细解释。这样一来,我对Kernel PCA 的计算过程有了更深刻的理解。
小壮: 不客气,如果还有其他问题,随时可以问我哦。
面试官: 明白了。那么,能否给一个实际应用中的例子,说明PCA的效果和用法?
小壮: 当然!比如在图像处理中,假设我们有一组人脸图像,通过PCA我们可以提取出人脸图像的主要特征,从而实现人脸识别或表情分析。这在降维的同时保留了关键信息,提高了算法的效率。
面试官: 嗯,还有什么需要补充的吗?
小壮: 最后,我想提到的是,在实际应用中,我们也可以利用Scree图(Scree plot)来帮助选择主成分数量。这张图会展示每个主成分的方差解释比例,通过观察拐点来判断保留的主成分数量。
具体实现的话。首先,我们先计算每个主成分的方差解释比例。这个比例可以通过每个特征值除以总特征值的和来得到。
接下来,对这些方差解释比例进行降序排列,得到一个降序排列的序列。然后,我们绘制Scree图,横轴是主成分的编号,纵轴是对应的方差解释比例。
面试官: 那我们可以看到什么样的图形呢?
小壮: 一个典型的Scree图是一个曲线逐渐下降的图形。在图中,我们可以观察到曲线的肘部,即曲线迅速下降趋势趋缓的位置。
假设我们有一个数据集,进行PCA后得到如下的方差解释比例:
$[0.45, 0.25, 0.1, 0.05, 0.03, 0.02, 0.01, 0.009, 0.008, 0.006]$
然后我们绘制Scree图,如下:
import matplotlib.pyplot as plt
# 方差解释比例
variance_explained = [0.45, 0.25, 0.1, 0.05, 0.03, 0.02, 0.01, 0.009, 0.008, 0.006]
# 绘制Scree图
plt.plot(range(1, len(variance_explained) + 1), variance_explained, marker='o')
plt.xlabel('Principal Components')
plt.ylabel('Variance Explained Ratio')
plt.title('Scree Plot')
plt.show()
在图中,我们可以观察到曲线在第2个主成分后迅速下降趋势趋缓,这个位置就是我们选择主成分数量的拐点。
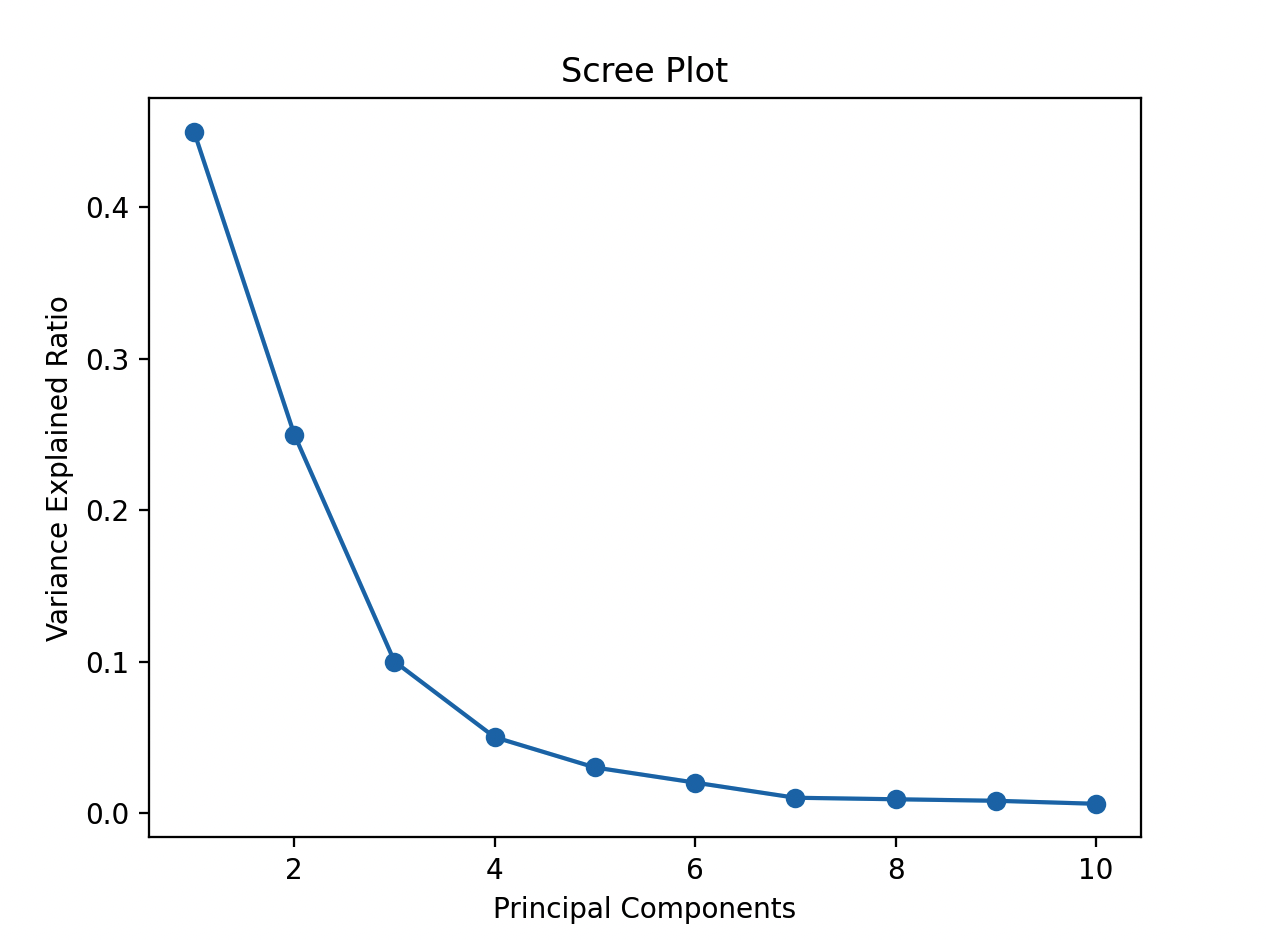

面试官: 明白了,这个图形清晰地展示了主成分数量选择的依据。咱们继续下一个话题~
小壮: 好的。
2、t-SNE相较于PCA有更强的局部保留能力,但在大规模数据上的计算开销较大。请说明在什么情况下选择使用t-SNE,以及如何通过调整超参数来平衡其计算效率和表达能力。
面试官: 小壮,你好。首先,想请你解释一下t-SNE和PCA的区别,以及在什么情况下你会选择使用t-SNE而不是PCA 这个问题?
小壮: 你好!当然,t-SNE和PCA都是降维技术,但它们的原理和适用场景有所不同。
PCA是线性降维方法,主要通过找到数据中的主成分来减少维度。相比之下,t-SNE是一种非线性降维方法,它能够更好地保留数据的局部结构。
在选择使用t-SNE的时候,我会考虑数据的复杂结构,特别是当数据存在非线性关系或者有明显的簇状结构时。t-SNE在保留局部关系方面表现得更好,能更清晰地展现数据内在的类别和相似性。
面试官: 在大规模数据上,t-SNE相对于PCA来说计算开销更大,怎么解决这个问题呢?
小壮: t-SNE的计算复杂度是二次的,主要来自于高斯核的相似度计算和梯度下降的迭代。为了解决大规模数据上的计算问题,我们可以采用一些策略。
首先,我们可以使用随机子采样来减少数据量,从而加速计算。其次,可以通过使用加速技术,如基于树结构的近似方法(如Barnes-Hut t-SNE),来降低计算复杂度。这些方法在维持相对较好的降维效果的同时,显著提升了计算速度。
面试官: 好的,那么具体说说t-SNE的原理,以及在什么情况下你会调整超参数来平衡计算效率和表达能力?
小壮: t-SNE的核心思想是将高维空间中的相似性映射到低维空间中的概率分布,然后通过最小化这两个空间中的分布差异来降维。具体来说,对于高维数据中的点$i$和点$j$,我们通过高斯分布计算它们在高维和低维空间中的相似概率。
在调整超参数时,我们主要关注两个参数:学习率(perplexity)和迭代次数。Perplexity控制了每个点附近的邻域大小,影响了t-SNE对局部结构的保留。较大的perplexity会考虑更远的点,而较小的则更注重局部结构。迭代次数则直接影响计算复杂度和收敛速度。
在实践中,我通常会先使用默认参数进行初始尝试,然后根据降维效果和计算开销的平衡情况来调整这两个超参数。例如,如果计算太慢,可以适当降低perplexity或减少迭代次数。
面试官: 再举个实际应用的例子吧!
小壮: 好的。比如说,我们有一个大规模的图像数据集,想要在二维空间中呈现出图像之间的相似性。这时候,t-SNE就派上用场了。它能够在降维的同时,保留图像的局部结构,使得相似的图像在低维空间中距离较近,更易于观察和理解。
我来简要展示一下t-SNE的数学公式和Python代码。
首先,t-SNE的高维空间中的相似概率计算公式:
$$
p_{ij} = \frac{\exp(-||x_i – x_j||^2 / 2\sigma_i^2)}{\sum_{k \neq i}\exp(-||x_i – x_k||^2 / 2\sigma_i^2)}
$$
其中,$\sigma_i$ 是高斯分布的标准差,由perplexity参数决定。
然后,低维空间中的相似概率计算公式:
$$
q_{ij} = \frac{(1 + ||y_i – y_j||^2)^{-1}}{\sum_{k \neq i}(1 + ||y_i – y_k||^2)^{-1}}
$$
最小化这两个分布之间的KL散度,就是t-SNE的优化目标。
下面是一个简化版的Python代码,使用了scikit-learn库:
import numpy as np
from sklearn.datasets import make_blobs
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
# 生成一些示例数据
X, y = make_blobs(n_samples=300, centers=3, random_state=42)
# 创建t-SNE模型
tsne = TSNE(n_components=2, perplexity=30, n_iter=300, random_state=42)
# 在低维空间中拟合数据
low_dimension = tsne.fit_transform(X)
# 绘制结果
plt.scatter(low_dimension[:, 0], low_dimension[:, 1], c=y, cmap='viridis')
plt.title('t-SNE Visualization')
plt.xlabel('Dimension 1')
plt.ylabel('Dimension 2')
plt.show()
这个简单的例子展示了如何使用t-SNE对高维数据进行降维,并在二维空间中呈现出数据的结构。

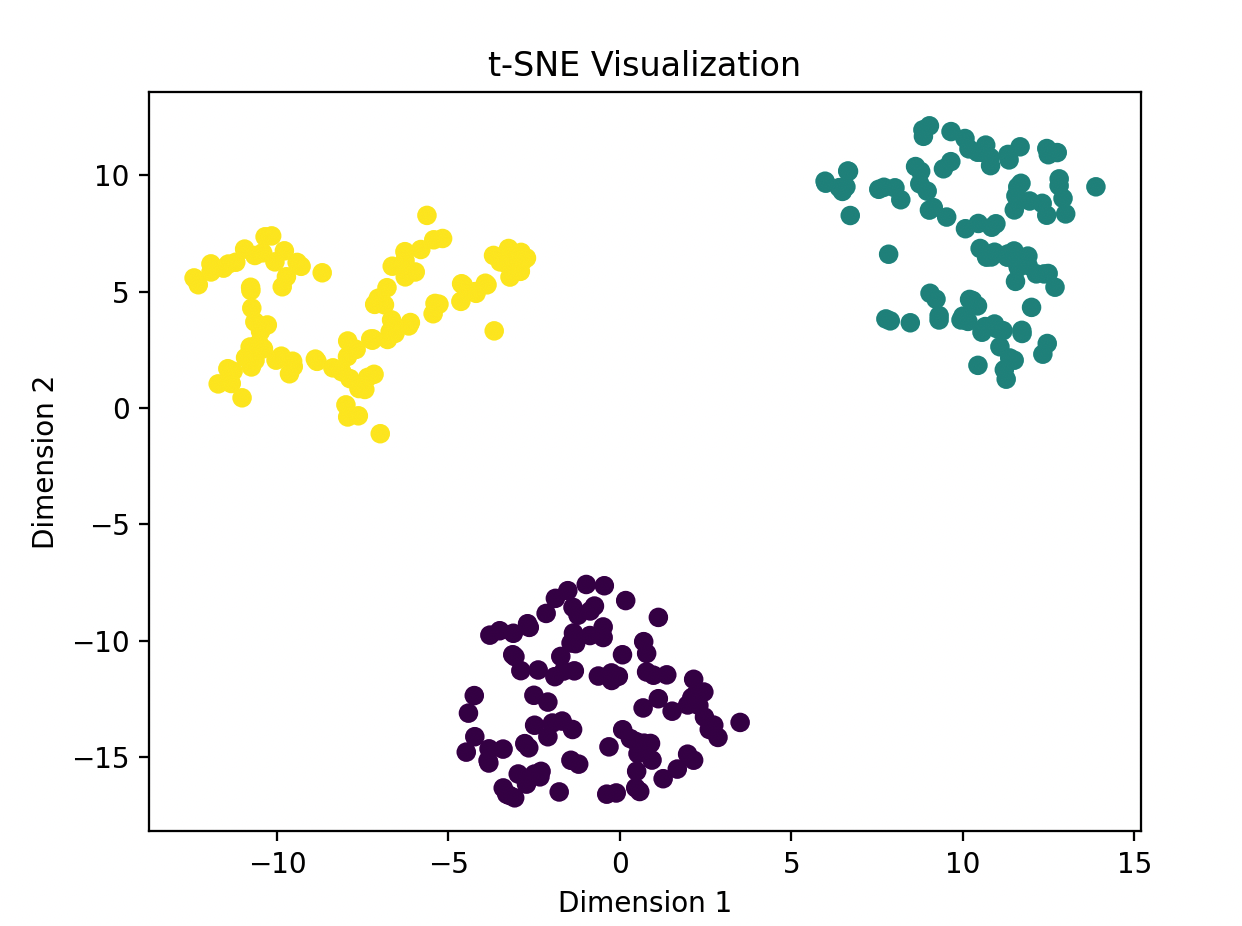
面试官: 好的,咱们继续~
小壮: 好的。
3、详细解释独立成分分析的盲源分离原理,以及在实际应用中,如何处理可能存在的混合信号和非高斯性的数据分布。
**面试官: ** 接下来,咱们探讨一下独立成分分析的盲源分离原理。
小壮: 独立成分分析(ICA)的核心思想是在混合信号中找到相互独立的源信号。这种方法在处理混合信号时非常有用,比如音频信号中的混响和语音,或者图像中的多个独立物体。盲源分离则是指在不知道源信号的情况下进行分离。
面试官: 那么,具体来说,独立成分分析是如何实现盲源分离的呢?
小壮: 独立成分分析基于统计学原理,最大的难点在于找到一个线性变换矩阵,使得混合信号的独立成分能够通过这个变换被分离出来。这个过程可以通过最大似然估计来完成。
首先,我们设混合信号为 $X = AS$,其中 $X$ 是观测到的混合信号矩阵,$A$ 是混合矩阵,$S$ 是源信号矩阵。
我们的目标是找到矩阵 $W$,使得 $Y = WX$ 中的 $Y$ 的每一列都是相互独立的。这里的 $Y$ 就是经过独立成分分析后的信号矩阵。
面试官: 介绍一下这个过程中的数学原理。
小壮: 我们引入了一个常用的非高斯性度量 – 尖峰度(kurtosis),通过最小化尖峰度的方法来达到独立性。具体而言,我们要最大化下面这个目标函数:
$$
\max_W \, G(W) = \sum_{i=1}^n \left( kurt(Y_i) – \lambda \cdot h(kurt(Y_i)) \right)
$$
其中,$ kurt(Y_i) $ 是 $Y_i$ 列的尖峰度,$\lambda$ 是一个权重系数,$h(kurt(Y_i))$ 是一个修正项,目的是保证不同独立成分的尖峰度都能被充分考虑。
面试官: 有没有实际应用中的案例可以说明呢?
小壮: 当然。一个典型的例子是音频信号处理。想象一下在一个房间里有多个人在说话,录制的音频中混合了各种语音信号,还可能有背景噪音。通过独立成分分析,我们可以将这些不同的语音信号分离出来,实现单独的语音信号还原。
面试官: 那么在实际应用中,可能会遇到混合信号的非高斯性分布,你是如何处理的?
小壮: 混合信号的非高斯性分布确实是一个挑战。为了解决这个问题,我们通常采用对数似然函数,将问题转化为最小化一个非凸函数。这样,即使混合信号的分布非高斯,我们也可以通过迭代优化算法,比如快速独立成分分析算法(FastICA),来找到最优的分离矩阵。
面试官: 能详细介绍一下对数似然函数的转化过程吗?
小壮: 当然。对于非高斯分布,我们使用对数似然函数来求解最大化问题。对于一个源信号 $s_i$,我们假设它的非高斯性分布为 $g_i(u)$,那么对应的对数似然函数为:
$$
\ln p_i(u) = \ln | \frac{dg_i(u)}{du} | – \ln g_i(u)
$$
通过最小化整个混合信号的对数似然函数,我们就可以得到一个非高斯独立性的度量。
面试官: 这样一来,就可以处理非高斯性分布的混合信号了。有没有什么具体的计算步骤或者公式推导可以展示一下呢?
小壮: 当我们定义混合信号的对数似然函数 $L(W)$ 时,我们实际上是在建立一个衡量混合信号分离效果的指标。对数似然函数的目标是最大化,通过最大化这个函数,我们能够找到使得混合信号的独立成分尽可能独立的分离矩阵 $W$。
具体而言,对于一个观测到的混合信号 $X$,我们假设其生成过程为 $X = AS$,其中 $A$ 是混合矩阵,$S$ 是源信号。我们要找到一个分离矩阵 $W$,使得通过 $Y = WX$ 的线性变换后,得到的 $Y$ 的每一列都是相互独立的。这就是我们的优化目标。
为了衡量独立性,我们引入了源信号的非高斯性度量。对于源信号 $s_i$,我们假设其非高斯性分布为 $g_i(u)$。对应的对数似然函数为:
$$
\ln p_i(u) = \ln | \frac{dg_i(u)}{du} | – \ln g_i(u)
$$
这里,$u$ 是源信号经过线性变换后的值,即 $u = W^T x_i$,其中 $x_i$ 是观测到的混合信号的第 $i$ 列。通过最小化整个混合信号的对数似然函数 $L(W)$:
$$
L(W) = \sum_{i=1}^n \left( \ln | \frac{d g_i(W^T x_i)}{d (W^T x_i)} | – \ln g_i(W^T x_i) \right)
$$
我们就在统计学上追求使得混合信号的源信号在非高斯性上达到最大的独立性。在这个优化过程中,我们通过迭代算法,比如梯度下降,来调整矩阵 $W$,使得对数似然函数最大。
这个过程中,我们通过最小化对数似然函数来实现对混合信号的盲源分离,而非高斯性度量则是用来表达我们对独立性的统计假设。
面试官: 具体的实现中,你是否可以分享具体的相关代码出来?
小壮: 当然,我可以展示一段基于FastICA的Python代码:
import numpy as np
def g(u):
# 非高斯性分布的假设函数,可以根据具体问题选择
return np.tanh(u)
def dg(u):
# 假设分布的导数
return 1 - np.tanh(u)**2
def fast_ica(X, max_iter=1000, tol=1e-4):
n, m = X.shape
W = np.eye(n) # 初始化权重矩阵为单位矩阵
for _ in range(max_iter):
W_old = W.copy()
Y = np.dot(W, X)
Y_g = g(Y)
Y_dg = dg(Y)
W = (X @ Y_g.T - np.diag(Y_dg.sum(axis=1)) @ W) / m + W
# 使用正交化方法,保证 W 的正交性
W = np.linalg.qr(W)[0]
# 检查收敛条件
if np.linalg.norm(W - W_old) < tol:
break
return W
# 使用示例
X = np.random.rand(3, 1000) # 生成随机混合信号
A = np.random.rand(3, 3) # 随机混合矩阵
S = A @ X # 得到源信号
# 添加非高斯性,模拟真实场景
S[0, :] = np.tanh(S[0, :])
S[1, :] = np.sin(S[1, :])
S[2, :] = S[2, :]**3
# 执行FastICA
W = fast_ica(S)
# 得到分离后的信号
Y = W @ S
# 打印结果
print("混合矩阵 A:\n", A)
print("\n分离矩阵 W:\n", W)
这段代码演示了如何使用FastICA来分离混合信号。在实际应用中,我们需要根据具体问题选择合适的非高斯性分布函数和其导数。这个例子中使用的是双曲正切函数。
面试官: 解释的非常好!咱们继续~
小壮: 好的。
4、层次聚类有自上而下和自下而上两种方法,它们各自的优势是什么?在处理具有不同规模和形状的簇时,层次聚类如何应对?
面试官: 你好,小壮!层次聚类有两种方法,一种是自上而下的划分法,另一种是自下而上的凝聚法。你能详细说明它们各自的优势吗?
小壮: 当然可以!自上而下的划分法是从整体开始,将数据集划分成不同的子集,然后逐步细化,形成聚类结构。这种方法的优势在于它能够快速地处理大规模数据,因为它首先将整个数据集划分成相对均衡的子集,然后再逐步深入细分。而且,由于是自上而下的过程,可以更容易地提前设定层次结构,对于某些特定领域的应用比较有针对性。
面试官: 那么,自下而上的凝聚法呢?
小壮: 自下而上的凝聚法相反,它从单个数据点开始,逐步合并相似的数据点,直到整个数据集被合并成一个簇。这种方法的优势在于它能够发现不同尺度和形状的簇,因为它是通过合并相似数据点来逐步形成聚类结构的。这种方法更适合处理数据集中存在明显层次结构的情况,例如生物学中的分类问题。
面试官: 明白了。那么在处理具有不同规模和形状的簇时,层次聚类有什么策略来应对呢?
小壮: 当处理具有不同规模的簇时,层次聚类通常使用一些链接准则,比如单链接、完全链接或平均链接来衡量簇的相似度。对于不同形状的簇,我们可以使用不同的距离度量,比如欧氏距离、曼哈顿距离或者相关系数,以适应不同的数据结构。这样能够在聚类过程中更好地处理不同尺度和形状的簇。
面试官: 那么,具体来说,你能给一个例子来说明吗?
小壮: 当然!比如我们有一个数据集包含两个不同尺度的簇,一个大的簇A和一个小的簇B。如果我们使用平均链接作为相似度度量,那么在合并簇的过程中,平均链接会考虑簇A和簇B中所有点的平均距离,而不仅仅是簇A和簇B之间的距离。这样就能够处理不同尺度的簇,确保在聚类过程中不会因为簇的规模不同而产生偏差。
面试官: 在处理不同形状的簇时呢?
小壮: 对于不同形状的簇,我们可以选择适当的距离度量来反映数据点之间的相似性。比如,如果我们的数据集包含球形簇和椭球形簇,使用欧氏距离可能会更适合处理球形簇,而马氏距离可能更适合处理椭球形簇。这样能够更好地适应不同形状的簇结构。
面试官: 那么在层次聚类中,具体的计算步骤是怎样的呢?
小壮: 嗯,层次聚类的计算步骤主要包括初始化,计算相似度矩阵,选择最相似的簇进行合并,更新相似度矩阵,重复以上步骤直到得到最终的聚类结构。我来详细解释一下。
首先,我们初始化每个数据点为一个簇。然后,我们计算相似度矩阵,该矩阵记录了每对簇之间的相似度。这里可以使用不同的相似度度量,如欧氏距离或相关系数。
接下来,我们选择相似度矩阵中最小的值,对应于最相似的两个簇,将它们合并成一个新的簇。然后,更新相似度矩阵,计算新合并的簇与其他簇之间的相似度。
重复以上步骤,直到只剩下一个簇为止,这样就得到了最终的聚类结构。
面试官: 这个流程很清晰。还有一个问题,你能否推导一下层次聚类中相似度矩阵的更新公式?
小壮: 当然可以。在层次聚类中,更新相似度矩阵的公式通常涉及到链接准则。以单链接为例,相似度矩阵的更新公式可以表示为:
$$
D_{ij} = \min(D_{ik}, D_{jk})
$$
这里,$D_{ij}$ 表示簇 $i$ 和 $j$ 之间的相似度,而 $D_{ik}$ 和 $D_{jk}$ 分别表示簇 $i$ 和 $k$ 之间、簇 $j$ 和 $k$ 之间的相似度。
这个公式的直观解释是:在合并簇 $i$ 和 $j$ 后,它们的相似度 $D_{ij}$ 取决于它们在簇 $k$ 中的最相似程度。也就是说,我们选择簇 $k$ 中与簇 $i$ 或 $j$ 最相似的那个簇,作为新合并的簇与其他簇的相似度。这确保了在层次聚类的过程中,我们每次合并都选择了最相似的簇,按照最小链接的方式逐步形成聚类结构。
面试官: 明白了。在实际应用中,你有没有使用过层次聚类的例子?
小壮: 必须有!比如在图像分割中,层次聚类可以用来将相邻的像素点合并成具有相似颜色的区域,从而实现图像的分割。这对于识别图像中的对象边界非常有效。
下面的Python代码,给出的是如何使用层次聚类进行图像分割。
import numpy as np
from scipy.cluster.hierarchy import linkage, dendrogram
import matplotlib.pyplot as plt
# 生成示例数据
np.random.seed(0)
data = np.random.rand(10, 2)
# 层次聚类
linkage_matrix = linkage(data, method='average')
# 绘制树状图
dendrogram(linkage_matrix)
plt.title('Hierarchical Clustering Dendrogram')
plt.xlabel('Data points')
plt.ylabel('Distance')
plt.show()
使用层次聚类对随机生成的二维数据进行聚类,并绘制出树状图以展示聚类结构。

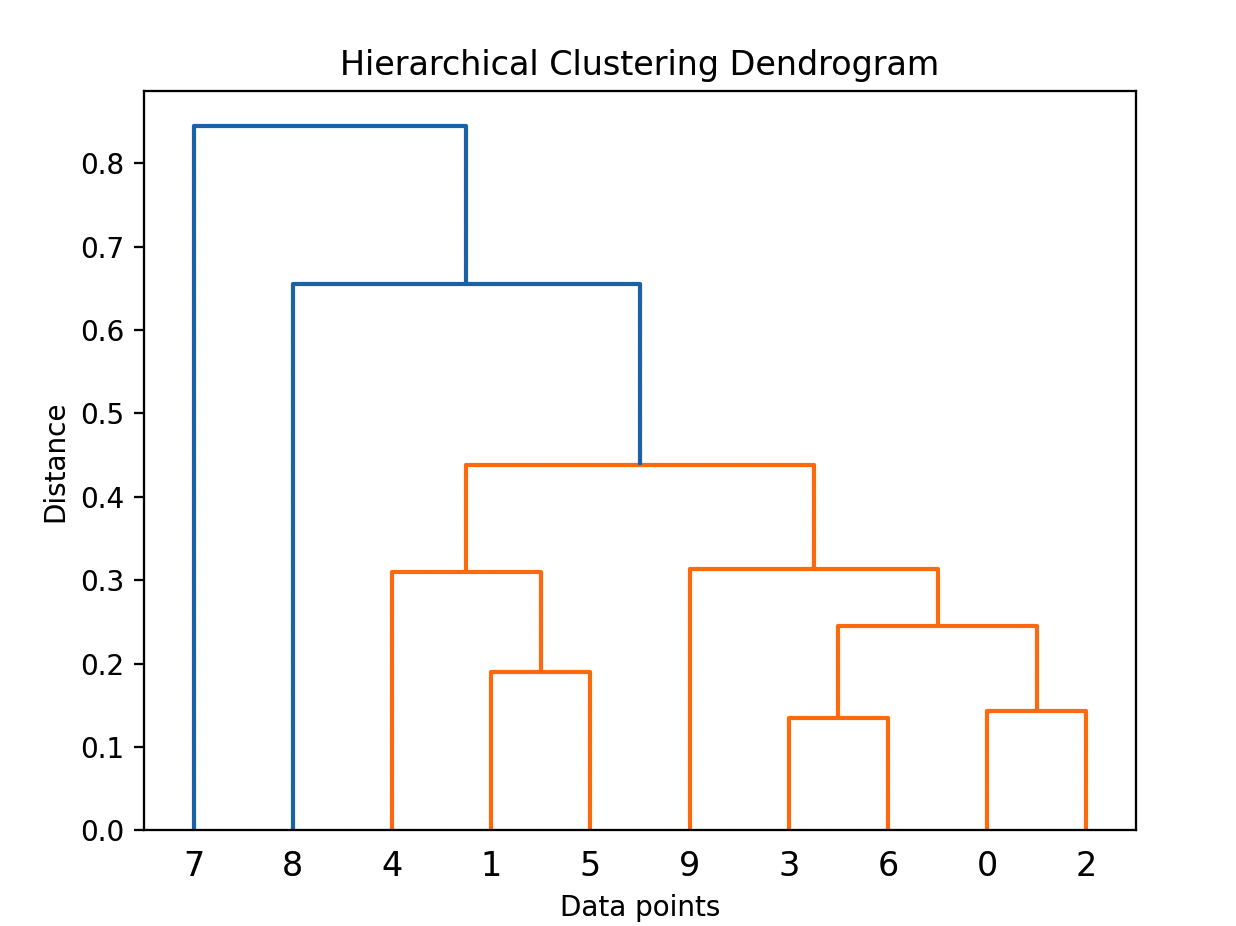
面试官: 非常棒。最后一个问题,你认为层次聚类在哪些场景中更适用,而在哪些场景中可能不太适用呢?
小壮: 嗯,层次聚类适用于一些数据具有层次结构的场景,比如图像分割、生物学领域的分类等。它也对于不知道聚类数量的情况下很有优势。在处理小规模数据和具有明显层次结构的情况下,层次聚类效果较好。
但是,对于大规模数据集,层次聚类的计算复杂度较高,可能不太适用。此外,在数据集的簇结构比较复杂或者簇的形状差异较大时,层次聚类的效果可能会受到影响。因此,合适的聚类方法要根据具体的应用场景和数据特点来选择。
面试官: 非常感谢你的回答,小壮!
小壮: 谢谢!
5、详细解释DBSCAN中的核心概念,包括核心对象、密度可达和密度相连。另外,请讨论在选择适当的ε和MinPts时可能面临的挑战。
面试官: 小壮,首先,能否详细解释一下DBSCAN中的核心概念,包括核心对象、密度可达和密度相连?
小壮: 您好!DBSCAN的核心概念非常关键。在DBSCAN中,一个核心对象是在半径ε内至少包含MinPts个数据点的对象。这意味着核心对象拥有足够的邻居,可以成为一个聚类的中心。MinPts的设定是为了确保核心对象具有一定的密度,而不是孤立的点。
密度可达是一个基础概念,表示如果点A在点B的ε邻域内,并且点B是核心对象,那么点A就密度可达于点B。这说明点A可以通过一系列相邻的核心对象,逐步达到点B。这个过程是一种密度连接的方式,有点像“跳跃式”的密度链接,通过局部密度的增加来构建聚类结构。
最后,密度相连是一个传递关系,如果点A与点B密度可达,点B与点C也是密度可达,那么点A与点C就是密度相连的。这个特性保证了聚类的连通性,即聚类内的点都可以通过密度可达关系连接在一起,形成紧密的簇。
面试官: 了解了核心概念,那在选择适当的ε和MinPts时可能面临的挑战是什么?
小壮: 嗯,选取合适的ε和MinPts确实是个挑战。首先,ε的选择直接影响簇的形状和数量。如果选取较小的ε,可能将噪声点误认为是簇的一部分;而如果选取较大的ε,可能将不同簇的点合并在一起。MinPts的选择也是一个权衡,选择过小可能导致大量的噪声点,而选择过大可能导致将簇分裂成多个小簇。
面试官: 明白了,那你能详细解释一下如何选择适当的ε和MinPts吗?
小壮: 当然。一种方法是通过可视化数据,观察不同参数下的聚类效果。这样可以帮助我们直观地了解算法对数据的划分情况。另外,还有一种称为”Knee Point”的方法,通过绘制ε和MinPts的关系图,找到拐点,即聚类数开始保持稳定的点。
$$
\text{Knee Point} = \text{arg min}_{(x, y)}\left[\frac{\text{d}^2(y)}{\text{d}x^2}\right]
$$
这个式子表示我们通过找到聚类数曲线的凹点来确定拐点。在这个拐点处对应的MinPts值即为我们要选择的参数。
面试官: 你能给个实际案例或者计算步骤来说明吗?
小壮: 当然,我们可以用一个简单的Python示例来演示。假设我们有一组二维坐标点数据:
from sklearn.cluster import DBSCAN
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
# 生成一些随机数据
X, _ = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)
# 使用DBSCAN进行聚类
dbscan = DBSCAN(eps=0.3, min_samples=5)
labels = dbscan.fit_predict(X)
# 可视化结果
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis')
plt.title('DBSCAN Clustering')
plt.show()
这里我们设置了ε为0.3,MinPts为5。通过调整这两个参数,观察聚类效果的变化。

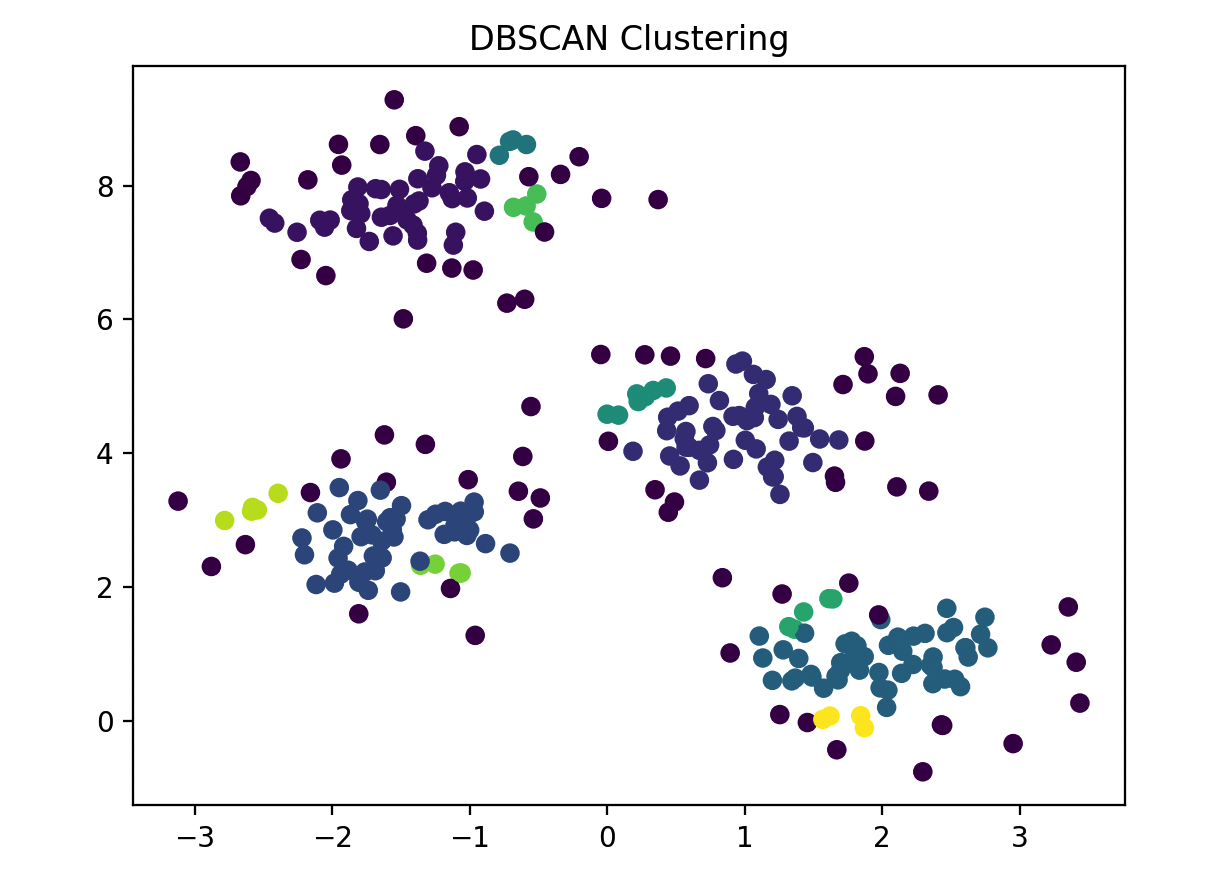
面试官: 非常好,咱们继续~
小壮: 好的。
6、GMM与K均值聚类相比,更适用于建模不同形状和大小的簇。请解释GMM的EM算法用于参数估计的步骤,并说明在什么情况下它可能陷入局部最优。
面试官: 小壮,咱们继续。聊聊GMM与K均值聚类相比,更适用于建模不同形状和大小的簇。能解释一下GMM的EM算法用于参数估计的步骤吗?
小壮: 好的,当然可以。GMM的EM算法包含四个关键步骤:初始化、E步、M步和收敛检查。
面试官: 嗯,那咱们从初始化说起。
小壮: 初始化阶段的目标是确定每个高斯分布的均值、协方差矩阵和混合系数。这一步可以使用随机选择、K均值聚类结果或者其他启发式方法完成。
在E步骤中,我们计算每个数据点属于每个分布的后验概率。这是通过应用贝叶斯公式实现的。对于第i个数据点和第j个高斯分布,后验概率的计算公式如下:
$$
P(z_j|x_i) = \frac{P(x_i|z_j)P(z_j)}{\sum_{k=1}^{K} P(x_i|z_k)P(z_k)}
$$
这里,$z_j$表示数据点属于第j个高斯分布的事件,$P(x_i|z_j)$为第j个高斯分布生成第i个数据点的概率,$P(z_j)$为选择第j个高斯分布的先验概率,K为总的高斯分布数量。
M步骤涉及参数的更新。对于每个高斯分布,我们更新均值、协方差矩阵和混合系数。具体的公式如下:
均值的更新:
$$
\mu_j = \frac{\sum_{i=1}^{N} P(z_j|x_i)x_i}{\sum_{i=1}^{N} P(z_j|x_i)}
$$
协方差矩阵的更新:
$$
\Sigma_j = \frac{\sum_{i=1}^{N} P(z_j|x_i)(x_i – \mu_j)(x_i – \mu_j)^T}{\sum_{i=1}^{N} P(z_j|x_i)}
$$
混合系数的更新:
$$
\pi_j = \frac{\sum_{i=1}^{N} P(z_j|x_i)}{N}
$$
这里,$N$为数据点的总数。
面试官: 非常详细,那收敛检查呢?
小壮: 收敛检查通常通过观察似然函数值的变化或者参数的变化情况来进行。如果似然函数值在迭代中趋于稳定,或者参数的变化小于某个阈值,我们可以认为算法已经收敛。
面试官: 那在什么情况下,GMM的EM算法可能陷入局部最优?
小壮: 这是一个深入的问题。EM算法有一些局限性,尤其在初始参数选择上容易受到影响。具体来说,GMM的EM算法可能陷入局部最优的情况主要有两个方面的考虑。
首先,EM算法对于初值非常敏感。如果我们选择的初始参数离真实值较远,可能导致算法在优化过程中陷入局部最优解。这种情况在高维空间中尤为显著,因为存在更多的参数组合可能导致相同的似然函数值。
其次,GMM的优化问题是一个凸优化问题,但EM算法并不保证全局最优。EM算法只能保证收敛到一个局部最优解。这是由于EM算法的迭代过程,每次迭代只是在当前参数空间内搜索,可能错过全局最优点。
为了应对这些挑战,我们通常会采用一些启发式方法进行初始化,比如使用K均值聚类结果初始化GMM的参数。这有助于提高算法收敛到全局最优的可能性,但并不能完全消除陷入局部最优的风险。
总体而言,选择合适的初始化策略、增加迭代次数以及多次运行算法并选择效果最好的结果等方法都是降低陷入局部最优风险的有效手段。
面试官: 嗯,所以对于GMM的应用,初始化是关键。
小壮: 没错!好的初始化有助于避免陷入局部最优。一种常用的方法是使用K均值聚类的结果来初始化GMM的参数。
面试官: 明白了。能用一个实际案例来说明吗?
小壮: 当然可以,我这里构建一个更具体的案例。假设我们有一个二维数据集,其中包含两个簇:一个呈椭圆形,另一个是圆形。我们想利用GMM对这个数据进行聚类。
小壮: 假设我们用K均值聚类进行初始化,它可能会将两个簇都初始化为圆形簇,因为K均值聚类不考虑簇的形状差异。
import numpy as np
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
# 生成椭圆形簇的数据
np.random.seed(0)
theta = np.linspace(0, 2*np.pi, 100)
ellipse_cluster = np.array([2*np.cos(theta), 1*np.sin(theta)]).T
ellipse_cluster += np.random.normal(scale=0.1, size=ellipse_cluster.shape)
# 生成圆形簇的数据
circle_cluster = np.random.normal(scale=0.1, size=(100, 2))
# 合并两个簇的数据
data = np.concatenate([ellipse_cluster, circle_cluster])
# 使用K均值聚类初始化
kmeans = KMeans(n_clusters=2, random_state=0)
kmeans_labels = kmeans.fit_predict(data)
# 可视化
plt.scatter(data[:, 0], data[:, 1], c=kmeans_labels, cmap='viridis', marker='.')
plt.title('K-Means Clustering Initialization Result')
plt.show()

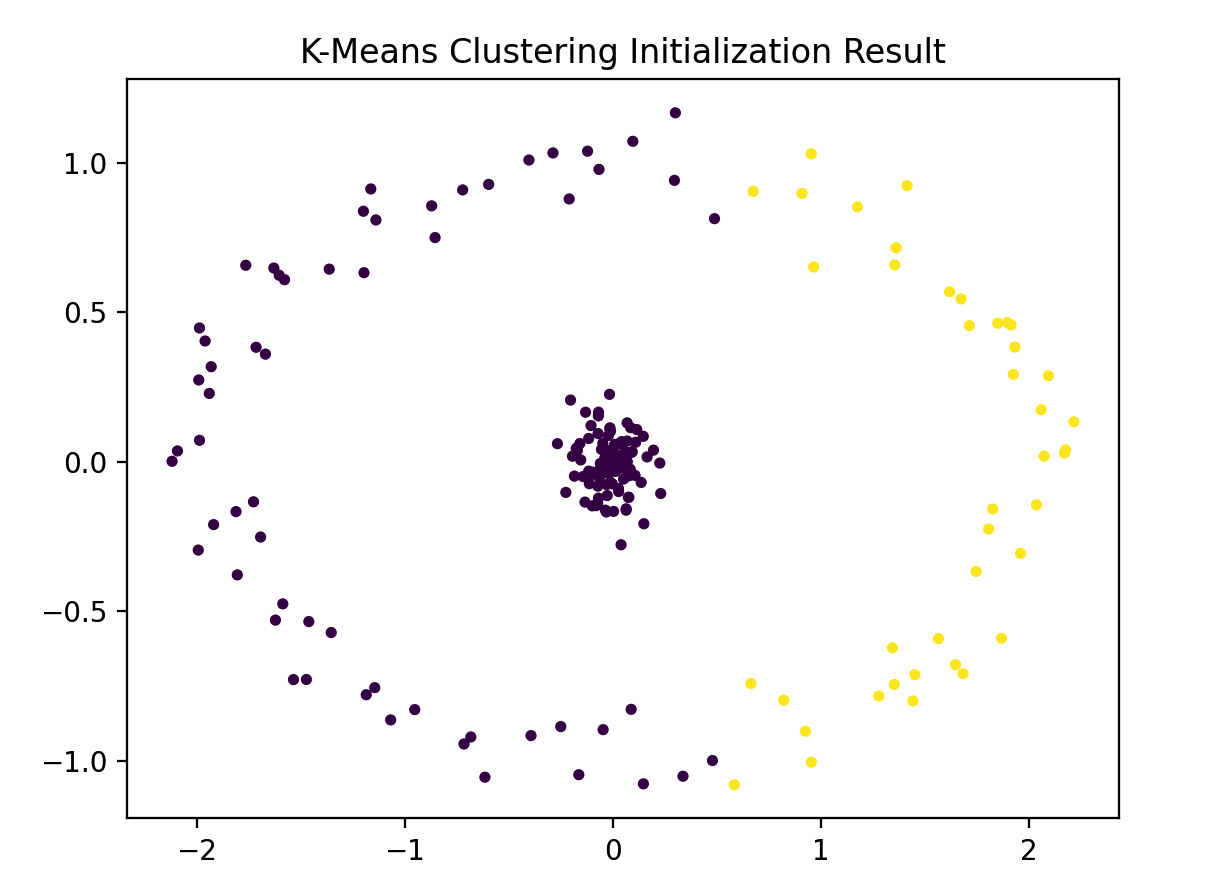
面试官: 很直观,这里K均值聚类初始化的结果都是圆形簇。那么接下来会发生什么呢?
小壮: 正是这个问题。如果我们用这样的初始化来运行GMM的EM算法,由于它对簇的形状和大小有一定假设,可能会导致算法陷入局部最优。
现在,让我们用EM算法进行进一步的操作:
from sklearn.mixture import GaussianMixture
# 使用K均值聚类结果初始化GMM
gmm = GaussianMixture(n_components=2, means_init=kmeans.cluster_centers_, random_state=0)
gmm_labels = gmm.fit_predict(data)
# 可视化
plt.scatter(data[:, 0], data[:, 1], c=gmm_labels, cmap='viridis', marker='.')
plt.title('GMM EM Algorithm Result')
plt.show()

面试官: 看起来是不是有点问题?
小壮: 是的,这里GMM EM算法的结果可能会偏向于其中一个圆形簇。因为初始化将两个簇都设为圆形,而实际上存在一个椭圆形簇。这就是陷入局部最优的一个例子。
面试官: 这么说,如果我们采用更智能的初始化方法,问题就能得到解决?
小壮: 对的,例如,我们可以利用层次聚类或密度聚类的结果来更合理地初始化GMM。这样,初始参数更接近真实情况,有助于算法更容易收敛到全局最优解。
面试官: 哦,明白了。感谢的解释。
小壮: 不客气。
7、LSTM通过引入遗忘门和输入门解决了梯度消失问题,但它也有一些可能存在的问题。请讨论在训练LSTM时可能面临的挑战以及针对这些挑战的解决方法。
面试官: 咱们继续,我们知道LSTM通过引入遗忘门和输入门来解决梯度消失问题,但在实际训练中,你认为可能会面临哪些挑战呢?
小壮: 虽然LSTM在处理梯度消失问题上表现优异,但在训练时仍然存在一些挑战。首先,让我简单解释一下LSTM在PyTorch中的基本点。
LSTM引入了遗忘门(forget gate)和输入门(input gate),通过控制信息的流动来减轻梯度消失问题。遗忘门用于决定前一时刻的记忆状态中哪些信息应该被遗忘,而输入门则用于控制新的输入信息加入记忆状态。这两者的协同作用有效地解决了长序列上的梯度消失问题。
面试官: 那么,在训练LSTM时,你觉得可能会面临哪些挑战呢?
小壮: 在训练LSTM时,一个常见的挑战是梯度爆炸问题。梯度爆炸通常发生在反向传播过程中,由于网络深度或者长时间依赖性,导致梯度值变得非常大,难以稳定地进行参数更新。具体来说,梯度爆炸的问题可以通过以下公式表示:
$$
\text{梯度更新} = \text{学习率} \times \text{梯度}
$$
如果梯度过大,梯度更新的幅度就会变得很大,可能导致参数值迅速增加,最终无法收敛。
此外,还有遗忘门和输入门的权重初始化问题。不合适的初始权重可能导致网络无法捕捉到有效的信息,影响整个模型的性能。
面试官: 确实是值得关注的问题。你有什么解决这些挑战的方法吗?
小壮: 对于梯度爆炸问题,一种有效的方法是梯度裁剪(gradient clipping),通过设置一个阈值,限制梯度的大小,防止其爆炸。这可以在优化器中进行简单的设置,如下所示:
import torch
import torch.optim as optim
# 创建一个带梯度裁剪的优化器
optimizer = optim.Adam(model.parameters())
torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=1.0)
对于权重初始化问题,可以采用一些经典的初始化方法,如Xavier/Glorot初始化,确保权重在适当的范围内初始化。
import torch.nn.init as init
# 使用Xavier初始化
init.xavier_uniform_(lstm.weight_ih_l0)
init.xavier_uniform_(lstm.weight_hh_l0)
这两种方法可以帮助缓解训练中的梯度爆炸问题和权重初始化问题。
面试官: 非常具体的建议,小壮。在解决这些问题的同时,你有没有考虑过模型的拓展性和泛化性呢?
小壮: 当然,面试官。在训练LSTM时,我们还需要考虑到模型的拓展性和泛化性。一个可能的挑战是过拟合,特别是在数据量较小的情况下。为了解决这个问题,我们可以采用正则化技术,如Dropout,通过在训练过程中随机关闭一些神经元来减小过拟合的风险。
import torch.nn as nn
# 在LSTM层中添加Dropout
lstm = nn.LSTM(input_size, hidden_size, dropout=0.2)
这样可以增加模型的泛化能力。此外,合适的数据增强技术也是一个有效的手段,通过对训练数据进行随机变换,增加模型对不同输入的适应能力。
面试官: 这些确实是提高模型性能的有效手段。不过,你提到的正则化和数据增强可能会引入新的问题,对吧?
小壮: 是的,正则化和数据增强可能会导致模型在训练过程中收敛缓慢,增加训练时间。为了解决这个问题,我们可以使用一些加速训练的技术,如批标准化(Batch Normalization)。
import torch.nn as nn
# 在LSTM层中添加Batch Normalization
lstm = nn.LSTM(input_size, hidden_size)
bn = nn.BatchNorm1d(hidden_size)
这可以加速训练收敛,并提高模型的稳定性。当然,具体的调参和选择合适的超参数也是至关重要的。
面试官: 在实际应用中,我们可能还会遇到一些非平稳时间序列的情况,对吧?
小壮: 是的,非平稳时间序列可能导致模型在训练时难以收敛。为了解决这个问题,我们可以考虑差分(differencing)操作,将非平稳时间序列转化为平稳序列。
这可以通过以下代码实现:
import numpy as np
# 差分操作
def difference(data):
return np.diff(data)
# 示例
original_sequence = [1, 3, 6, 10, 15]
stationary_sequence = difference(original_sequence)
这样,我们就能更好地处理非平稳时间序列的情况。
面试官: 除了这些,你还有其他考虑过的训练中的挑战和解决方法吗?
小壮: 当然,还有一点我想提到的是长序列训练中的记忆问题。在处理非常长的序列时,LSTM可能会遗忘早期时刻的信息,导致长期记忆能力下降。为了解决这个问题,我们可以考虑使用注意力机制(Attention Mechanism),使模型能够更好地关注重要的时间步。
import torch.nn as nn
# 在LSTM层中添加Attention Mechanism
lstm = nn.LSTM(input_size, hidden_size, attention=True)
这样,模型就能够更灵活地处理长序列,提高长期记忆的性能。
面试官: 不错,咱们继续~
小壮: 好的。
8、词袋模型忽略了词语的顺序和语法结构。在实际应用中,如果需要考虑文本的上下文信息,你会选择使用哪种文本表示方法,以及为什么?
面试官: 小壮,我想问你一个关于文本表示方法的问题。词袋模型忽略了词语的顺序和语法结构,在实际应用中,如果需要考虑文本的上下文信息,你会选择使用哪种文本表示方法,以及为什么?
小壮: 这是一个很有深度的问题。词袋模型的确在一些场景表现得不太尽如人意。如果我们要考虑文本的上下文信息,我会选择使用Word Embeddings(词嵌入)来进行文本表示。Word Embeddings 能够捕捉词汇之间的语义关系,让我们更好地理解文本的语境。
面试官: 你能详细解释一下Word Embeddings是如何工作的吗?
小壮: Word Embeddings基于分布式表示学习,它将每个词映射到一个高维实数向量,这个向量能够捕捉到词语的语义信息。其中最典型的例子是Word2Vec模型。这个模型通过训练一个神经网络来学习词语的分布式表示。
首先,定义一个目标函数,最大化一个词语上下文的概率,这样模型就能够学到词语在语境中的语义。我们可以使用以下公式来表示:
$$
P(w_t | w_{t-1}, w_{t-2}, \ldots, w_{t-n+1})
$$
这表示在给定前面$n-1$个词语的条件下,预测第$t$个词语的概率。
对数似然函数为:
$$
\log P(w_t | w_{t-1}, w_{t-2}, \ldots, w_{t-n+1})
$$
通过梯度下降法最大化这个对数似然函数,我们就能够得到词向量。
面试官: 好的,明白了。那有没有实际应用的例子,你能说明一下Word Embeddings是如何捕捉上下文信息的吗?
小壮: 比如,我们有两个句子,“猫在床上”和“狗在沙发上”。在词袋模型中,这两句话被视为完全不同,因为它们的词语顺序不同。而在Word Embeddings中,这两个句子可能会有相似的词向量,因为“猫”和“狗”在语境中可能扮演相似的角色。
这是因为Word Embeddings学到的向量空间中,语义相近的词在空间中距离较近,能够更好地反映词语之间的关系。
面试官: 好的,你的解释很清晰。但是,有时候我们会遇到一些长文本,如何处理长文本的上下文信息呢?
小壮: 长文本的处理确实是一个难点。为了解决这个问题,我们可以使用更先进的模型,比如Long Short-Term Memory (LSTM) 或者 Gated Recurrent Unit (GRU)。这些模型被设计用来捕捉长序列中的依赖关系,特别适用于处理长文本的上下文信息。
面试官: LSTMs和GRUs是什么,它们是如何工作的呢?
小壮: 哈哈,这就涉及到循环神经网络(RNN)的领域啦。LSTM和GRU都是RNN的一种改进,能够更好地处理长序列的信息。
LSTM引入了一个记忆单元(memory cell)来存储长期记忆,同时通过三个门(输入门、遗忘门和输出门)来控制信息的流动。GRU也类似,但只有两个门(更新门和重置门)。
在LSTM中,更新规则可以表示为:
$ f_t = \sigma(W_f \cdot [h_{t-1}, x_t] + b_f) $
$ i_t = \sigma(W_i \cdot [h_{t-1}, x_t] + b_i) $
$ o_t = \sigma(W_o \cdot [h_{t-1}, x_t] + b_o) $
$ \tilde{c}t = \tanh(W_c \cdot [h{t-1}, x_t] + b_c) $
$ c_t = f_t \odot c_{t-1} + i_t \odot \tilde{c}_t $
$ h_t = o_t \odot \tanh(c_t) $
这里,$\sigma$ 表示 sigmoid 函数,$\odot$ 表示逐元素相乘,$[h_{t-1}, x_t]$ 表示连接 $h_{t-1}$ 和 $x_t$。
面试官: ok,通过一个简单的例子来说明一下~
小壮: 假设我们要预测一个句子中下一个词的概率,我们可以使用一个LSTM模型。比如,给定前两个词“我”和“爱”,我们想要预测下一个词。
首先,我们将“我”和“爱”通过Embedding层转换成向量表示,然后输入到LSTM中。LSTM会根据当前的上下文状态输出一个概率分布,我们可以通过Softmax函数得到最可能的下一个词。
如果我们的训练数据中有句子“我爱吃冰淇淋”,模型经过训练后,应该能够更好地理解上下文,预测下一个词是“冰淇淋”。
这就是LSTM通过学习上下文信息来预测文本的一种方式。
面试官: 好的,最后,你认为在实际应用中,选择使用Word Embeddings和LSTM的场景有哪些呢?
小壮: 一般来说,如果我们处理的是静态文本,比如情感分析、文本分类等,使用Word Embeddings效果很好,因为它能够更好地捕捉词语之间的语义关系。
而对于涉及到长序列的任务,比如机器翻译、文本生成等,LSTM就很有优势,因为它可以更好地处理长文本的上下文信息。
当然,有时候我们也可以将它们结合使用,比如在预训练模型中使用Word Embeddings,然后在任务特定的模型中使用LSTM进行 fine-tuning,这样能够充分发挥它们各自的优势。
面试官: 小壮,非常好!
小壮: 谢谢!
9、Word2Vec和GloVe是两种流行的词嵌入方法,它们的训练策略有何异同?如何根据应用场景选择合适的词嵌入模型?
面试官: 小壮,你对于Word2Vec和GloVe这两种词嵌入方法的了解,首先,简要介绍一下它们的训练策略有何异同吗?
小壮: 你好。Word2Vec和GloVe都是用于将词汇映射到连续向量空间的词嵌入方法。它们的主要区别在于训练策略。
小壮: Word2Vec有两种模型,Skip-gram和CBOW。其中,Skip-gram模型通过给定中心词预测上下文词,而CBOW则相反,通过上下文词预测中心词。训练时,通过最大化条件概率来优化模型参数。
以Skip-gram为例,给定语料库中的序列$(w_1, w_2, …, w_T)$,最大化似然函数:
$$
L(\theta) = \prod_{t=1}^{T} \prod_{-c \leq j \leq c, j \neq 0} P(w_{t+j} | w_t; \theta)
$$
其中,$P(w_{t+j} | w_t; \theta)$是条件概率,$\theta$是模型参数。
小壮: GloVe的训练策略,主要思想是通过全局语料统计信息来学习词嵌入。其目标是最小化词向量的点乘和与共现矩阵词频的差异。
其损失函数如下:
$$
J = \sum_{i=1}^{V} \sum_{j=1}^{V} f(P_{ij}) (\mathbf{w}i^T \cdot \mathbf{w}_j + b_i + b_j – \log(P{ij}))^2
$$
其中,$P_{ij}$是词 $i$ 和词 $j$ 的共现次数,$\mathbf{w}_i$和$\mathbf{w}_j$是对应的词向量,$b_i$和$b_j$是两个词的偏置项,$f(x)$是权重函数,常用的是截断的二次函数。
面试官: 那么在实际应用中,你会如何选择合适的词嵌入模型呢?
小壮: 好问题!选择合适的模型通常取决于应用场景。如果我们的应用需要关注上下文信息,比如在机器翻译或情感分析中,Word2Vec 的 Skip-gram 模型可能更合适。因为它能够捕捉到词汇的语境信息,更好地表达词语之间的关系。
而如果我们的应用更注重全局语料的统计信息,比如在共现矩阵的频繁项集分析中,GloVe可能更为合适。它在保留全局统计信息的同时,可以更好地处理稀疏共现矩阵。
面试官: 明白了。那么在实际的工程应用中,你是如何调优这些模型的参数的呢?
小壮: 对于Word2Vec,通常需要调整的参数包括窗口大小、向量维度、学习率等。而GloVe中,除了模型中的维度和学习率,我们还需要关注权重函数的选择以及截断参数的设定。
在调优过程中,我会先使用一小部分数据进行快速训练和验证,然后逐步扩大数据规模进行调整。对于Word2Vec,我还会关注负采样的数量,这个参数在训练速度和模型性能之间有很大的影响。
面试官: 很详细。最后一个问题,你能给出一个实际应用中你成功使用Word2Vec或GloVe的案例吗?
小壮: 当然,一个典型的案例是在搜索引擎中的查询扩展。通过利用Word2Vec,我们可以把用户的查询扩展到语义相关的词汇,提高搜索的准确性和覆盖范围。举个例子,当用户输入“巴黎餐厅”,模型可能会推荐类似“法国美食”、“巴黎美食”等相关的词汇,从而丰富搜索结果。
而在GloVe的应用中,我曾经在文档分类任务中使用过,通过学习文档中词汇的全局统计信息,得到更加紧凑而具有语义信息的表示,从而提升了分类器的性能。
面试官: ok,咱们继续~
小壮: 好的。
10、为什么在模型评估中使用交叉验证是一个好的实践?在具体应用中,你是如何选择交叉验证的折数和划分方式的?
面试官: 小壮,接下来。我想了解一下你对于在模型评估中使用交叉验证的看法。为什么认为这是一个好的实践呢?
小壮: 交叉验证在模型评估中的应用是为了更全面、准确地评估算法的性能。一般而言,我们将数据集分为训练集和测试集,但这样有可能导致模型对于某个特定的划分过于敏感。交叉验证通过多次随机划分数据集,进行训练和测试,能够更稳健地评估模型的性能,避免了单次划分可能带来的偶然性。
面试官: 那么,对于交叉验证的折数和划分方式,你是如何选择的呢?
小壮: 嗯,这个问题涉及到一些取舍。首先,折数的选择要考虑到计算成本和模型稳定性。通常情况下,5折或者10折交叉验证是比较常见的选择。折数过多可能会增加计算负担,而折数过少可能不足以充分评估模型的泛化性能。
面试官: 折数主要考虑计算成本和模型稳定性。那么,划分方式呢?
小壮: 是的。对于划分方式,一般有三种:随机划分、分层划分和分组划分。随机划分是简单随机将数据分成训练集和测试集;分层划分保证了每个类别在训练集和测试集中的比例相似;而分组划分则是根据数据中的分组信息,确保同一组的样本不同时出现在训练集和测试集中。
面试官: 这么说,划分方式是为了避免某些特殊情况对模型评估的影响?
小壮: 对的。不同的问题和数据集可能适合不同的划分方式。比如,在医学领域,我们可能更倾向于分层划分,以确保各种病例在训练集和测试集中都有代表性。
面试官: 那么,能给我具体展示一下交叉验证的计算步骤和公式吗?
小壮: 当然。我们以 5 折交叉验证为例,假设数据集总共有N个样本。首先,将数据分成5份,每份的大小为N/5。然后,进行5轮训练和测试,每轮选其中一份作为测试集,其余4份作为训练集。计算每轮的性能指标,最后取平均值作为最终性能指标。
数学表示如下:
$$
\text{性能指标} = \frac{1}{5} \sum_{i=1}^{5} \text{性能指标}_i
$$
其中,性能指标可以是准确率、精确度等,具体取决于问题的要求。
面试官: 最后,你能展示一段Python代码,演示如何实现交叉验证吗?
小壮: 当然可以。这里是一个简单的例子:
from sklearn.model_selection import cross_val_score, KFold
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_digits
# 使用sklearn中的手写数字数据集作为例子
digits = load_digits()
X, y = digits.data, digits.target
# 创建随机森林分类器
model = RandomForestClassifier()
# 创建5折交叉验证
kf = KFold(n_splits=5, shuffle=True, random_state=42)
# 使用交叉验证计算准确率
accuracy_scores = cross_val_score(model, X, y, cv=kf, scoring='accuracy')
# 输出平均准确率
print("平均准确率:", accuracy_scores.mean())
# 平均准确率: 0.9760662333642834
这段代码使用了RandomForestClassifier作为模型,通过KFold进行5折交叉验证,最后输出了平均准确率。
面试官: 解释的非常好。
小壮: 非常感谢!
11、ROC曲线和AUC值通常用于二分类问题的性能评估。请解释在多类别分类问题中如何扩展和解释ROC曲线,并讨论AUC值的局限性。
面试官: 小壮,咱们再聊聊,你对于在多类别分类问题中如何扩展和解释ROC曲线有什么了解吗?
小壮: 好的,多类别分类问题中的ROC曲线扩展起来略有不同。首先,我们得知道在二分类中,ROC曲线描述了不同阈值下真正例率(True Positive Rate,TPR)与假正例率(False Positive Rate,FPR)之间的权衡。曲线越接近左上角,说明模型性能越好,因为此时TPR高而FPR低。
而AUC值则是ROC曲线下的面积,即曲线与坐标轴之间的面积。AUC值越接近1,说明模型性能越好。在多类别分类中,AUC值的微平均和宏平均提供了对整体性能的度量。
对于微平均,它考虑了所有类别的真正例和假正例的总体表现,相当于对每个类别赋予了相同的权重。而宏平均则是对每个类别的AUC值进行简单平均,对每个类别平等对待。
面试官: 能详细解释一下这两种策略吗?
小壮: 当然!首先是一对一策略,对于K个类别,我们组合任意两个类别,构建K * (K-1) / 2个二分类分类器,每个分类器解决一个类别与另一个类别之间的问题。接着,我们可以为每个分类器绘制ROC曲线,最后通过微平均(Micro-Averaging)或宏平均(Macro-Averaging)来得到整体的ROC曲线。
对于一对多策略,我们对每个类别都训练一个分类器,将其余所有类别作为负类。同样,通过绘制每个分类器的ROC曲线,最后进行平均操作来得到整体的ROC曲线。
面试官: 明白了。那AUC值在多类别问题中是如何计算的呢?
小壮: 好问题!在多类别情况下,AUC的计算方式取决于采用的微平均还是宏平均。对于微平均,我们将每个类别的真正例和假正例的数目相加,然后计算AUC。而对于宏平均,我们为每个类别分别计算AUC,最后取平均值。
来看一下公式。对于微平均:
$$
TPR_{\text{Micro}} = \frac{\sum_{i=1}^{K} \text{TP}i}{\sum{i=1}^{K} \text{P}_i}
$$
$$
FPR_{\text{Micro}} = \frac{\sum_{i=1}^{K} \text{FP}i}{\sum{i=1}^{K} \text{N}_i}
$$
$$
AUC_{\text{Micro}} = \frac{1}{K} \sum_{i=1}^{K} AUC_i
$$
而对于宏平均:
$$
AUC_{\text{Macro}} = \frac{1}{K} \sum_{i=1}^{K} AUC_i
$$
面试官: 解释得清楚。其它的有没有什么需要注意的地方?
小壮: 当然,AUC值也有其局限性。首先,它对于类别不平衡的问题较为敏感。如果某个类别的样本数量远远大于其他类别,AUC值可能会被主导,不够全面反映模型性能。其次,AUC无法提供类别间具体的排名信息,只是一个整体性能的度量。
而且,对于多类别问题,AUC的解释也相对复杂,需要结合具体情况进行综合评估。在实际应用中,我们常常需要综合考虑各种评价指标,如准确率、精确率、召回率等,来全面评估模型的性能。
最后,我想强调一下,在实际工程中,我们通常会使用专业的机器学习库来计算ROC曲线和AUC值,比如Scikit-Learn。这样可以避免重复造轮子,提高开发效率。
面试官: 小壮,我们刚才讨论了很多理论知识,现在我们来看看实际操作。你能给我展示一下如何用Python绘制多类别分类问题中的ROC曲线吗?
小壮: 当然可以!我们可以使用Scikit-Learn库中的roc_curve和auc函数。我先演示一下:
import numpy as np
from sklearn.metrics import roc_curve, auc
import matplotlib.pyplot as plt
from sklearn.preprocessing import label_binarize
from itertools import cycle
# 假设 y_true 和 y_score 是你的真实标签和预测结果
# 替换以下行为实际的数据
y_true = np.array([0, 1, 2, 0, 1, 2, 0, 2, 1, 2, 0, 1, 2, 1, 0])
y_score = np.array([[0.5, 0.2, 0.3],
[0.3, 0.4, 0.2],
[0.2, 0.3, 0.5],
[0.8, 0.1, 0.1],
[0.2, 0.6, 0.2],
[0.1, 0.2, 0.7],
[0.6, 0.2, 0.2],
[0.2, 0.2, 0.6],
[0.3, 0.4, 0.3],
[0.4, 0.3, 0.3],
[0.7, 0.1, 0.2],
[0.2, 0.5, 0.3],
[0.1, 0.3, 0.6],
[0.4, 0.3, 0.3],
[0.5, 0.2, 0.3]])
# 将标签进行二进制编码
n_classes = 3 # 假设有三个类别
y_true_binary = label_binarize(y_true, classes=range(n_classes))
# 初始化颜色循环
colors = cycle(['aqua', 'darkorange', 'cornflowerblue'])
# 初始化总体的TPR 和 FPR
mean_tpr = 0.0
mean_fpr = np.linspace(0, 1, 100)
# 计算每个类别的ROC曲线和AUC值
for i, color in zip(range(n_classes), colors):
fpr, tpr, _ = roc_curve(y_true_binary[:, i], y_score[:, i])
roc_auc = auc(fpr, tpr)
# 绘制ROC曲线
plt.plot(fpr, tpr, color=color, lw=2, label=f'ROC curve (class {i}), AUC = {roc_auc:.2f}')
# 对TPR进行插值,以便绘制平均ROC曲线
mean_tpr += np.interp(mean_fpr, fpr, tpr)
# 计算平均值并绘制平均ROC曲线
mean_tpr /= n_classes
mean_auc = auc(mean_fpr, mean_tpr)
plt.plot(mean_fpr, mean_tpr, color='navy', linestyle='--', lw=2, label=f'Mean ROC curve, Mean AUC = {mean_auc:.2f}')
# 绘制一些标志性的点和线
plt.plot([0, 1], [0, 1], color='gray', lw=2, linestyle='--', label='Random Guess')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Multi-Class ROC Curve')
plt.legend(loc='lower right')
plt.show()
这段代码可以绘制出每个类别的ROC曲线,并在图中标注AUC值。最后还绘制了平均的ROC曲线,以更全面地评估模型性能。

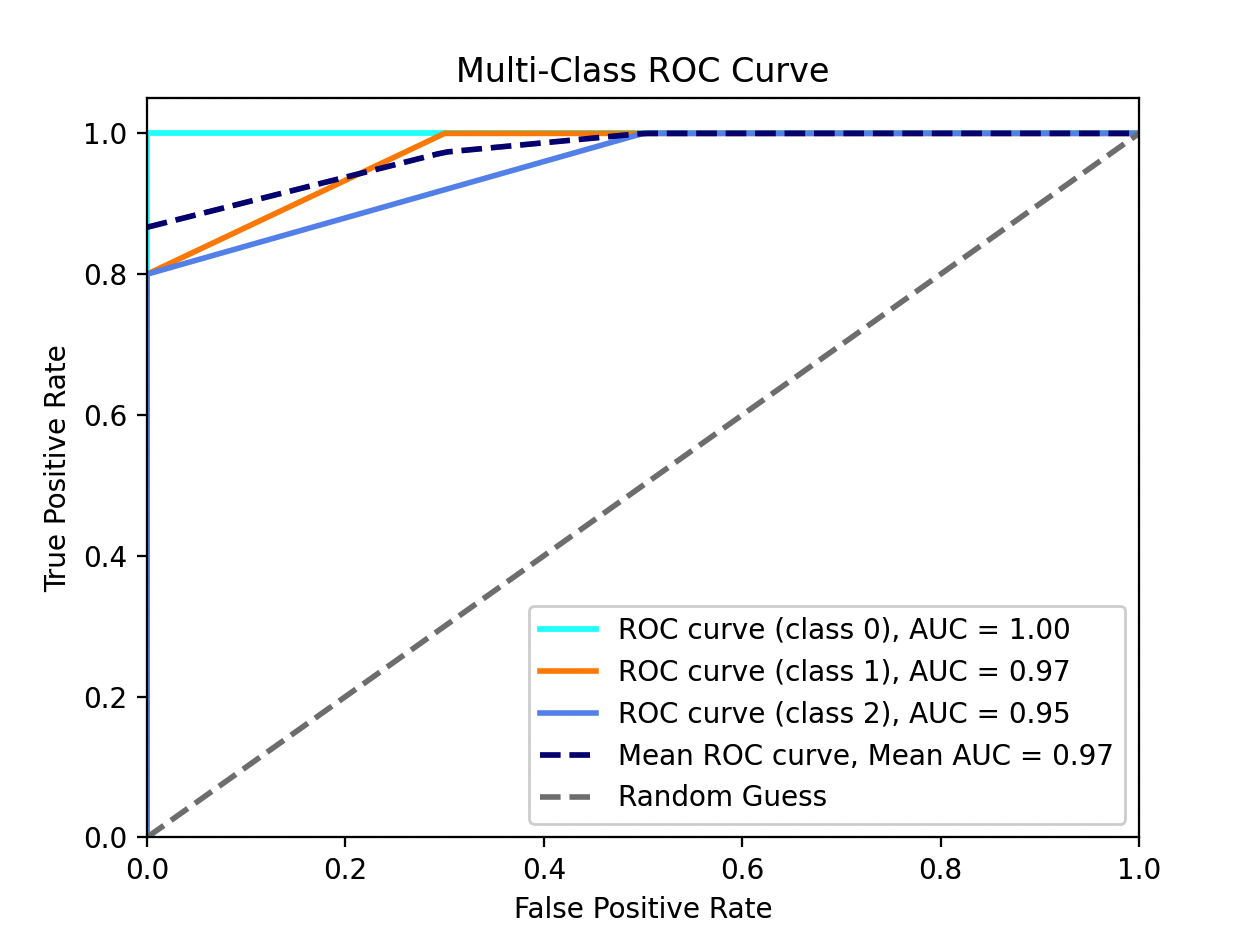
面试官: 太好了,小壮!那么对于AUC值的计算,能写个代码示例吗?
小壮: 当然,我这就给你演示:
from sklearn.metrics import roc_auc_score
from sklearn.preprocessing import label_binarize
import numpy as np
# 预测结果存储在y_score中,真实标签存储在y_true中
y_true = np.array([0, 1, 2, 0, 1, 2, 0, 2, 1, 2, 0, 1, 2, 1, 0])
y_score = np.array([[0.5, 0.2, 0.3],
[0.3, 0.4, 0.2],
[0.2, 0.3, 0.5],
[0.8, 0.1, 0.1],
[0.2, 0.6, 0.2],
[0.1, 0.2, 0.7],
[0.6, 0.2, 0.2],
[0.2, 0.2, 0.6],
[0.3, 0.4, 0.3],
[0.4, 0.3, 0.3],
[0.7, 0.1, 0.2],
[0.2, 0.5, 0.3],
[0.1, 0.3, 0.6],
[0.4, 0.3, 0.3],
[0.5, 0.2, 0.3]])
# 将标签进行二进制编码
y_true_binary = label_binarize(y_true, classes=[0, 1, 2]) # 假设有三个类别
# 计算每个类别的AUC值
auc_scores = []
for i in range(n_classes):
auc_i = roc_auc_score(y_true_binary[:, i], y_score[:, i])
auc_scores.append(auc_i)
print(f'AUC for class {i}: {auc_i:.2f}')
# 计算平均AUC值
mean_auc = np.mean(auc_scores)
print(f'Mean AUC: {mean_auc:.2f}')
# AUC for class 0: 1.00
# AUC for class 1: 0.97
# AUC for class 2: 0.95
# Mean AUC: 0.97
这段代码会计算每个类别的AUC值并打印出来,最后计算平均AUC值。
面试官: 很好!我们来看看下一个问题~
小壮: 好的。
12、为了提高模型的解释性,你会选择哪种类型的模型?在深度学习模型中,有哪些方法可以增强其可解释性,尤其是在处理图像或文本数据时?
面试官: 咱们最后一轮,为了提高模型的解释性,你会选择哪种类型的模型呢?
小壮: 对于提高模型解释性,我会倾向于选择一些简单而且可解释性强的模型,比如决策树或者线性模型。这样的模型通常更容易被理解和解释。
面试官: 那么在深度学习模型中,有哪些方法可以增强其可解释性,尤其是在处理图像或文本数据时呢?
小壮: 深度学习模型通常被认为是黑盒模型,但我们可以采用一些方法来提高其可解释性。首先,我们可以使用全局解释性方法,比如特征重要性分析。这通过分析模型中各个特征对输出的贡献来解释模型的决策。
面试官: 好的,具体来说,特征重要性分析是如何进行的呢?
小壮: 特征重要性分析通常通过计算特征的权重或重要性分值来实现。对于线性模型,权重就是特征的系数,而对于树模型,可以使用基尼系数或信息增益等。比如,对于线性回归模型,我们可以用以下公式计算权重:
$$
w_i = \frac{\sum_{j=1}^{N}(y_j – \hat{y_j}) \cdot x_{ij}}{\sum_{j=1}^{N}(x_{ij} – \bar{x_i})^2}
$$
其中,$w_i$ 是第 $i$ 个特征的权重,$N$ 是样本数量,$\hat{y_j}$ 是模型对第 $j$ 个样本的预测值,$x_{ij}$ 是第 $i$ 个特征在第 $j$ 个样本中的取值,$\bar{x_i}$ 是第 $i$ 个特征的均值。
面试官: 除了全局解释性方法,还有其他方法吗?
小壮: 当然,还有局部解释性方法,比如LIME(Local Interpretable Model-agnostic Explanations)。这个方法通过在输入空间中生成局部邻域,并在这个邻域内拟合一个简单的可解释模型,来解释模型的预测。对于图像或文本数据,可以通过对输入进行微小的扰动,生成近似的样本进行训练。
面试官: 你能详细说明一下LIME的工作原理吗?
小壮: 当然,LIME的核心思想是通过生成局部邻域样本,然后拟合一个线性模型来近似原始模型在这个邻域的表现。具体来说,对于图像数据,我们可以通过对原始图像进行像素级的扰动,生成一系列相似但略有变化的图像。然后,对于每个生成的图像,我们都使用原始模型进行预测,并记录输出。最后,通过拟合一个简单的线性模型来解释这些输出与原始输入之间的关系。
这个过程可以用以下公式表示:
$$
\hat{f}(x’) = \arg\min_{f’} \mathcal{L}(f, \pi_x) + \Omega(f’)
$$
其中,$\hat{f}(x’)$ 是对原始模型在邻域内的近似,$\mathcal{L}$ 是损失函数,$\pi_x$ 是在邻域内生成的样本,$\Omega$ 是正则化项。
面试官: 有没有其他方法可以增强深度学习模型的可解释性呢?
小壮: 当然,还有一种方法是使用递归神经网络(RNN)或注意力机制。在处理序列数据,如文本时,RNN可以提供一种逐步的解释方式,逐步显示模型对于每个时间步的关注点。而注意力机制则可以告诉我们在处理输入序列时模型关注的重点是什么。
面试官: 对于注意力机制,你能给个例子吗?
小壮: 比如在处理文本分类时,我们可以使用注意力机制来可视化模型对于每个词的关注程度。在这个过程中,我们可以计算每个词的权重,将其与原始文本相乘得到注意力分布,进而可视化模型在预测时关注的重点。
具体地,注意力分数的计算可以用以下公式表示:
$$
\alpha_i = \frac{\exp(e_i)}{\sum_{j=1}^{T}\exp(e_j)}
$$
其中,$\alpha_i$ 是第 $i$ 个词的注意力权重,$e_i$ 是对应的注意力分数。而注意力分数 $e_i$ 可以通过模型中的一些权重和激活值计算得到。
当然,还有一种常见的方法是使用可视化工具,比如Grad-CAM。这种方法通过计算损失函数对于模型最后一层输出的梯度,然后将这些梯度与最后一层的特征图相乘,得到每个像素的重要性分数。这可以用于生成图像的热力图,直观地展示模型在预测时关注的区域。
具体地,Grad-CAM的计算过程可以用以下公式表示:
$$
\text{{Grad-CAM}}(x, y_c) = \text{{ReLU}}\left(\sum_{k}\alpha_k^cA^k\right)
$$
其中,$\alpha_k^c$ 是梯度和特征图的权重,$A^k$ 是最后一层的特征图。
面试官: 总体来说,你认为在实际应用中,哪种方法更适合解释深度学习模型呢?
小壮: 在实际应用中,通常需要结合多种方法,根据具体问题选择最合适的解释方法。比如,对于图像分类任务,Grad-CAM可以提供直观的视觉解释,而对于文本分类任务,注意力机制可能更为合适。而如果需要全局解释,特征重要性分析和局部解释方法如LIME也可以同时使用,以全面理解模型的行为。
面试官: 很好。有没有其他方面的问题你想补充的呢?
小壮: 除了模型解释性,还有一些其他方面的问题,比如模型的鲁棒性、计算效率等,都是需要考虑的重要因素。在实际应用中,我们需要综合考虑多个方面来选择最合适的模型和方法。
面试官: 非常赞同,综合性思考是很重要的。
小壮: 谢谢面试官!

