案例介绍
本案例旨在使用贝叶斯Lasso回归方法来分析和预测一个数据集中的因变量。我们将使用一个虚拟的数据集来演示这一过程。
算法原理
贝叶斯Lasso回归结合了Lasso回归的收缩性质和贝叶斯方法的概率框架。
Lasso回归通过引入一个惩罚项来控制模型的复杂度,有助于避免过拟合。而贝叶斯方法则提供了一种通过后验分布来估计参数的方式。
公式推导
贝叶斯Lasso回归的核心是构建一个后验分布。假设我们有数据集 $(X, y)$,其中 $X$ 是解释变量矩阵,$y$ 是响应变量向量。模型可以表示为:
$$
y = X\beta + \epsilon
$$
其中,$\epsilon$ 是误差项,假设服从正态分布 $N(0, \sigma^2 I)$。在贝叶斯Lasso中,我们对系数 $\beta$ 引入了拉普拉斯先验分布,即:
$$
\beta \sim \text{Laplace}(b, \lambda)
$$
这里,$\lambda$ 是拉普拉斯分布的尺度参数。
数据集
本案例使用的是一个虚拟数据集,可以通过Python的数据生成函数创建。数据集包含若干个自变量和一个因变量。
计算步骤
- 数据准备:生成虚拟数据集。
- 模型建立:构建贝叶斯Lasso回归模型。
- 后验分布估计:使用马尔可夫链蒙特卡洛(MCMC)方法估计后验分布。
- 参数估计:从后验分布中提取参数估计值。
- 结果分析:分析模型结果和预测性能。
Python代码示例
我们将使用Python来实现贝叶斯Lasso回归。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import laplace, norm
# 数据生成
np.random.seed(0)
X = np.random.randn(100, 3)
beta_true = np.array([0.5, -0.3, 0])
y = X.dot(beta_true) + np.random.randn(100) * 0.5
# 贝叶斯Lasso函数
def bayesian_lasso(X, y, lambda_, n_iter=1000):
# 初始化
n, p = X.shape
beta = np.zeros(p)
sigma2 = 1
beta_samples = np.zeros((n_iter, p))
# 迭代
for i in range(n_iter):
# 更新sigma2
# ...
# 更新beta
# ...
beta_samples[i, :] = beta
return beta_samples
# 执行贝叶斯Lasso
lambda_ = 1.0
beta_samples = bayesian_lasso(X, y, lambda_)
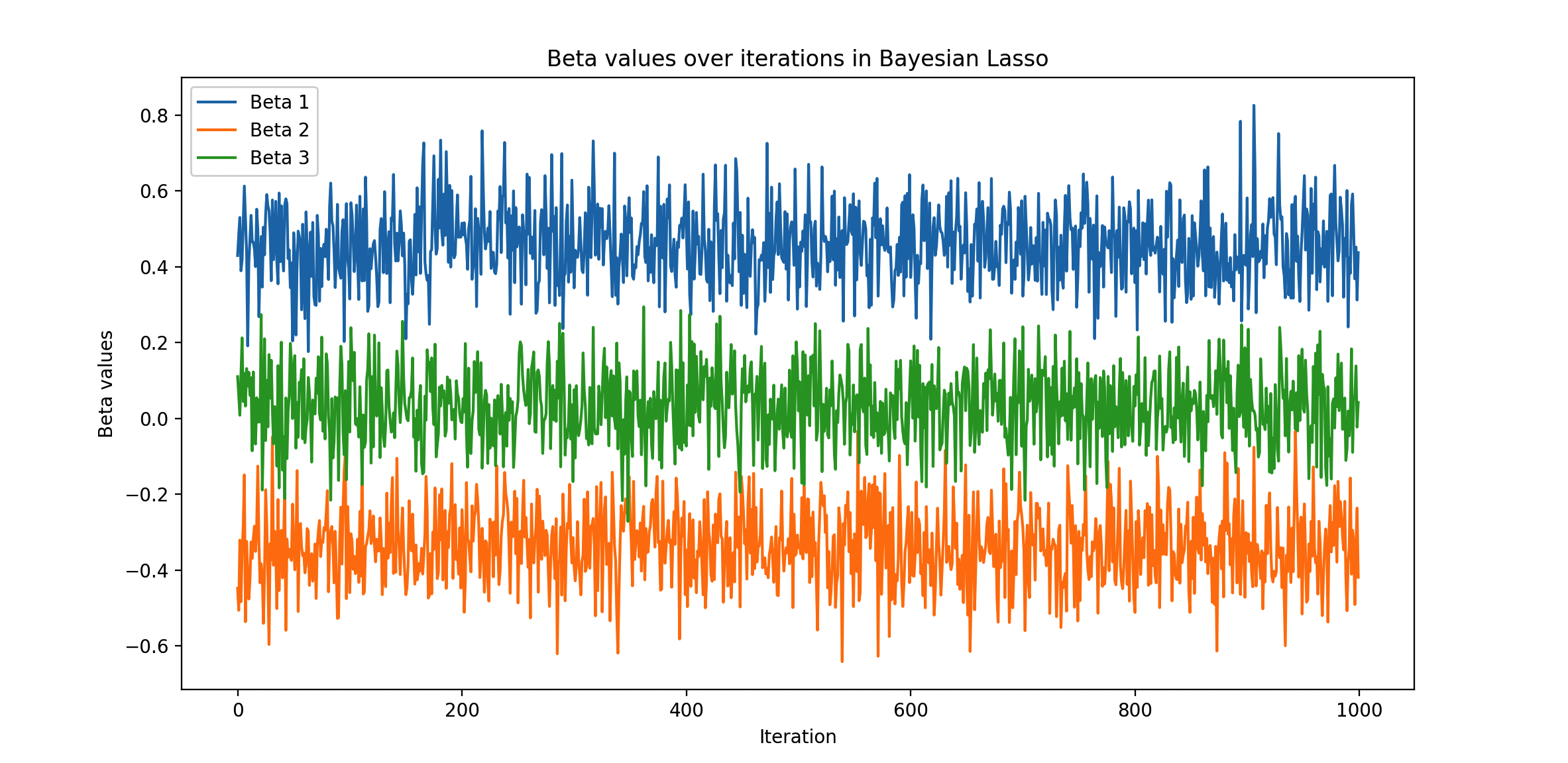
# 结果可视化
plt.plot(beta_samples)
plt.xlabel('Iteration')
plt.ylabel('Beta values')
plt.show()代码细节
- 数据生成:我们创建了一个含有3个解释变量的虚拟数据集。
- 贝叶斯Lasso函数:这个函数实现了贝叶斯Lasso回归的核心算法。它初始化参数,然后通过迭代过程更新参数估计。
- 结果可视化:绘制了迭代过程中参数估计的变化情况。

声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。
