2_多项式回归（Polynomial Regression）

案例介绍

在这个案例中，我们将使用多项式回归算法来预测波士顿地区房屋价格。我们有一些关于波士顿地区的房屋数据，包括房屋的各种特征（如房间数、附近学校的质量等）以及对应的房屋价格。我们将使用多项式回归模型来学习这些特征和价格之间的关系，并预测新的房屋价格。

算法原理

多项式回归是一种回归分析中使用的方法，可以通过拟合一个关于自变量的多项式来预测因变量的数值。与简单线性回归模型只使用一个自变量不同，多项式回归模型可以使用多个自变量来进行拟合。通过引入高次特征变量，多项式回归模型可以更好地适应非线性关系。

多项式回归模型的一般形式可以表示为：

$$
Y = \theta_0 + \theta_1X + \theta_2X^2 + \ldots + \theta_nX^n
$$

其中，$Y$表示因变量，$X$表示自变量，$\theta_0, \theta_1, \ldots, \theta_n$表示模型的参数，$n$表示多项式的阶数。

公式推导

为了推导多项式回归模型，我们考虑一个简单的二次多项式模型。假设我们有一组自变量 $X = \{x_1, x_2, \ldots, x_m\}$ 和对应的因变量 $Y = \{y_1, y_2, \ldots, y_m\}$，我们的目标是找到最佳拟合的二次多项式曲线。我们的模型形式为：

$$
Y = \theta_0 + \theta_1X + \theta_2X^2
$$

为了找到最佳拟合的参数值 $\theta_0, \theta_1, \theta_2$，我们可以使用最小二乘法。我们需要最小化残差平方和（RSS）：

$$
RSS = \sum_{i=1}^{m}(y_i – \hat{y}_i)^2
$$

其中，$y_i$是观测到的因变量值，$\hat{y}_i$是根据模型得到的预测值。

对于二次多项式模型，我们可以通过求解以下方程组得到参数值：

$$
\begin{bmatrix}
m & \sum X_i & \sum X_i^2 \\
\sum X_i & \sum X_i^2 & \sum X_i^3 \\
\sum X_i^2 & \sum X_i^3 & \sum X_i^4 \\
\end{bmatrix}
\begin{bmatrix}
\theta_0 \\
\theta_1 \\
\theta_2 \\
\end{bmatrix}
=
\begin{bmatrix}
\sum y_i \\
\sum X_iy_i \\
\sum X_i^2y_i \\
\end{bmatrix}
$$

求解该方程组即可得到最佳拟合的参数值。

数据集

为了完成这个案例，我们将使用波士顿房屋数据集。这个数据集包含了波士顿地区的房屋特征和价格信息。数据集包含506个样本和13个特征，可从sklearn.datasets模块中获取。

如果大家想要更换为读取本地数据文件，可以移步这里，看第二点https://www.ml-zhuang.club/5040/626/

计算步骤

1. 导入必要的库和数据集
2. 从数据集中加载波士顿房屋数据
3. 提取特征变量和目标变量
4. 使用多项式回归模型进行拟合
5. 预测新的房屋价格
6. 计算模型的性能指标（如均方误差）
7. 绘制原始数据散点图和拟合曲线图

Python代码示例

下面是用于完成上述步骤的完整Python代码。请确保安装了所需的库（如numpy、pandas、matplotlib和sklearn）。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

# 导入波士顿房屋数据集
boston = load_boston()

# 提取特征和目标变量
X = boston.data
y = boston.target

# 将特征向量转换为多项式特征
poly = PolynomialFeatures(degree=2)
X_poly = poly.fit_transform(X)

# 使用多项式回归模型进行拟合
model = LinearRegression()
model.fit(X_poly, y)

# 预测新的房屋价格
X_new = X[0].reshape(1, -1)
X_new_poly = poly.transform(X_new)
y_new = model.predict(X_new_poly)

# 计算模型的性能指标
y_pred = model.predict(X_poly)
mse = mean_squared_error(y, y_pred)

# 绘制原始数据散点图和拟合曲线图
plt.scatter(X[:, 0], y, color='blue', label='Actual')
plt.scatter(X_new[:, 0], y_new, color='red', label='Prediction')
plt.plot(X[:, 0], y_pred, color='green', label='Regression')
plt.xlabel('CRIM')
plt.ylabel('Price')
plt.legend()
plt.show()

print(f"Predicted price for new house: {y_new}")
print(f"Mean Squared Error: {mse}")

代码细节解释

1. 首先，我们导入了需要使用的库：numpy用于数值计算，pandas用于数据处理，matplotlib用于数据可视化，sklearn用于机器学习模型。
2. 然后，我们从sklearn.datasets模块加载了波士顿房屋数据集。
3. 接下来，我们提取了特征变量X和目标变量y。
4. 我们使用PolynomialFeatures类将原始特征向量X转换为多项式特征向量X_poly。在这个案例中，我们选择了二次多项式特征。
5. 使用LinearRegression类构建多项式回归模型并进行拟合。我们将多项式特征向量X_poly和目标变量y作为输入。
6. 接下来，我们使用训练好的模型预测新的房屋价格。为了演示目的，我们选择了原始数据集中的第一个样本X_new作为新的房屋特征。
7. 我们通过调用poly.transform()方法将新的特征向量X_new转换为多项式特征向量X_new_poly，然后将其输入到训练好的模型中预测房屋价格。
8. 计算模型的性能指标，如均方误差（MSE）。我们使用模型对所有样本的预测值和真实值来计算MSE。
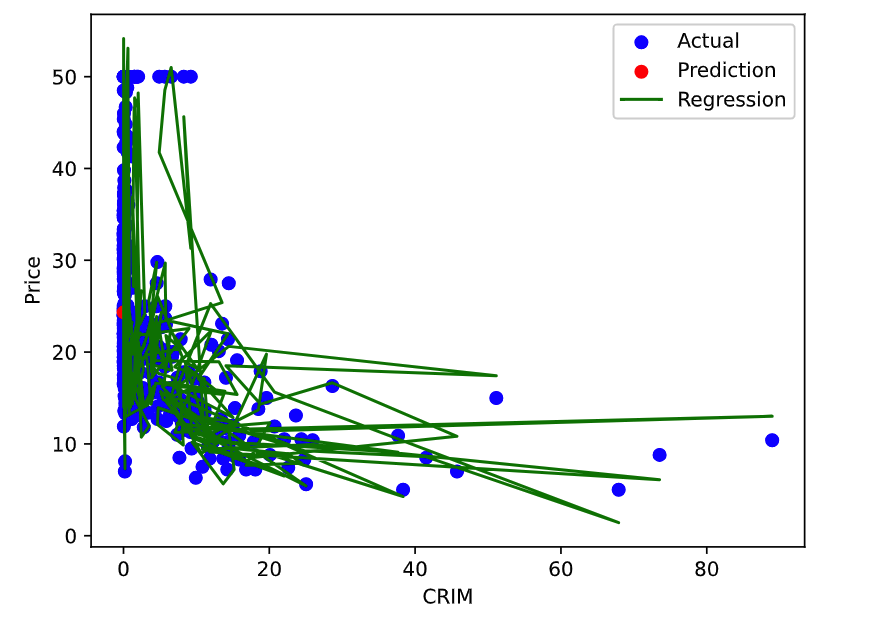
9. 最后，我们使用matplotlib库绘制了原始数据散点图和模型的拟合曲线图。蓝色散点图表示实际房屋价格，红色散点图表示模型预测的新房屋价格，绿色曲线是模型的拟合曲线。
10. 最后，我们打印出预测的新房屋价格和模型的均方误差。

这个案例展示了如何使用多项式回归模型来预测房屋价格，并使用波士顿房屋数据集进行演示。

cos大壮

海报 链接